アニーリングマシンのプログラミングのページでは、定式化された最適化問題をアニーリングマシン上で実行するまでの流れについて説明しました。ここでは実際にアニーリングマシンを利用して問題を解く例として、典型的な問題の1つである「巡回セールスマン問題」を挙げて説明します。巡回セールスマン問題とはどういう問題かについては量子アニーリング方式のページを参照してください。
QUBO 形式による表現 #
最適化問題を実際にアニーリングマシンを利用して解く為には、問題をQUBOやイジング形式のコスト関数によって表現する必要があります。具体例として、都市が4つの場合を例に挙げて説明します。
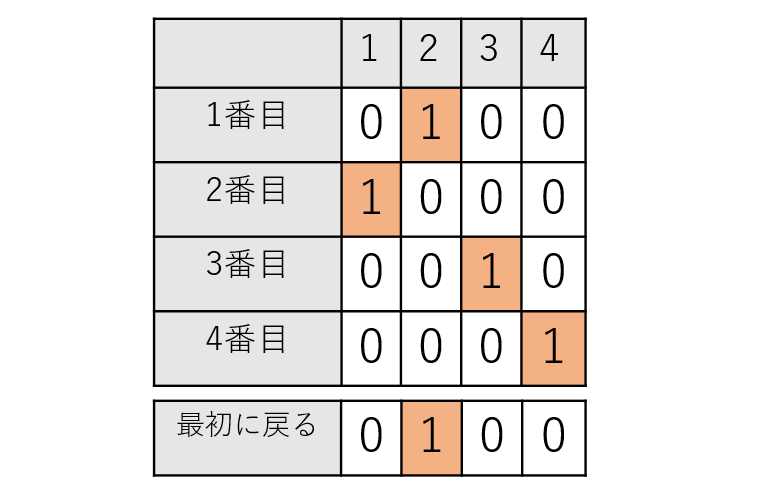
今回用いる方法では、まず都市数の2乗の数の変数を用意します。つまり、この場合は4の2乗で16個の変数が必要です。QUBO 形式では各変数は0か1のどちらかの値しか取ることができないため、これらの変数を図の上部分のように4×4の行列形式で並べ、「何番目に訪問するか」を行に、「どの都市を訪問するか」を列に対応させ、各変数は「 \(i\) 番目に都市 \(j\) を訪問する」を \(i\) 行 \(j\) 列の要素で表すという形を取ります。
例えば上の図の例では、1番目に都市2を訪問し、2番目に都市1を訪問し、といったように都市2→都市1→都市3→都市4→都市2の順で訪問することを表しています。
今回は文献1の方法に従い、次のようにしてコスト関数を構築しました。
総距離 #
巡回セールスマン問題におけるコスト関数は、ある順序で都市を回った場合の移動距離の総計です。移動距離を表す式は、先ほどの変数を用いると下記のようになります
\[L = \frac{1}{2}\sum_{a,i,j} d_{i,j}n_{a,i}(n_{a+1,j}+n_{a-1,j})\]\(L\) は総距離、 \(d_{i,j}\) は都市 \(i\) と都市 \(j\) の間の距離、 \(n\) は上図における各マス目に対応する QUBO 変数を表しています。 \(a\) は訪問順の番号を表します。先ほどの表に距離を表す相互作用を図示すると以下のようになります。
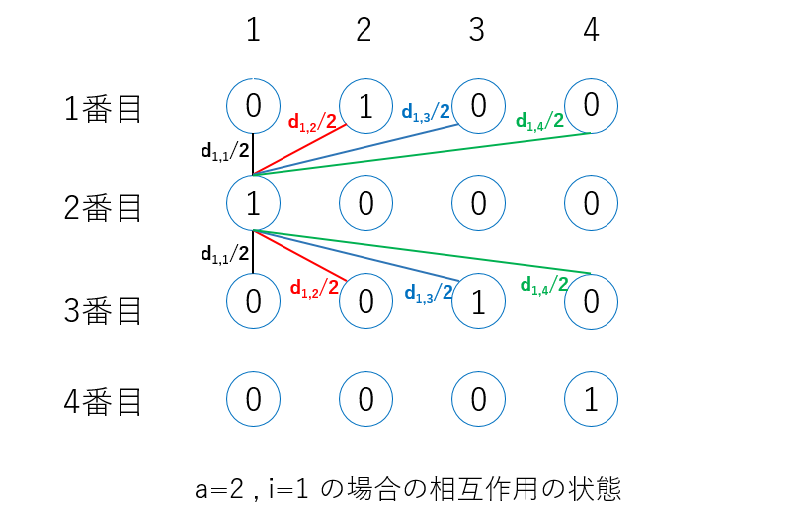
この相互作用を全ての \(a, i\) について合計すると、全ての経路を表現可能な総距離を表わす式になります。ここで、巡回セールスマン問題では最後に元の地点に戻ってこなければならないため、循環リストのように4行目と1列目は繋がっていると考えて設定する必要があります。
制約条件 #
このようにして、巡回セールスマン問題におけるコスト関数を QUBO 形式によって表現することができました。しかしながら、これだけでアニーリングマシンに送っても、正しく問題を解くことは出来ません。なぜならこのままでは、「同時に複数の都市を訪問してはならない」「複数回訪れたり、1度も訪れない都市があってはならない」という当たり前の制約が埋め込まれていないからです。そのため、これらの制約を破った状態が最適解になってしまわないように、制約条件を破った場合の罰則をコスト関数に与える必要があります。
この制約条件はつまり、「同じ行に1は1つしかない」「同じ列に1は1つしかない」です。以下の式が全ての行、列について成り立っているとき、制約条件が守られていることを意味します。
\[\sum_{a} n_{a,i} = 1\] \[\sum_{i} n_{a,i} = 1\]この制約条件を破る行、列が1つでもあった場合にコスト関数が増加するようにしたいので、右辺の \(1\) を左辺に移動し、負の項が出てこないように2乗を取ったものをコスト関数に加えます。
\[\sum_{i}(\sum_{a} n_{a,i} - 1)^2\] \[\sum_{a}(\sum_{i} n_{a,i} - 1)^2\]最終的なコスト関数 #
以上を踏まえ、最終的なコスト関数は以下の式のようになります。
\[H = \frac{1}{2}\sum_{a,i,j} d_{i,j}n_{a,i}(n_{a+1,j}+n_{a-1,j}) + k_1\sum_{i}(\sum_{a} n_{a,i} - 1)^2+k_2\sum_{a}(\sum_{i} n_{a,i} - 1)^2\]ここで、 \(k_1 > 0, k_2 > 0\) は制約条件の強さを表わす係数です。
グラフマッピング #
巡回セールスマン問題は、問題の構造上全結合を必要とします。そのため、D-Wave などの疎結合グラフ構造を持つアニーリングマシンに問題を載せる場合は、擬似的に全結合を作成するため使用できるビット数は少なくなります。2018年3月時点で最新の D-Wave 2000Q では、全結合を作成すると使用できるビット数は64ビットです。これは8都市の巡回セールスマン問題に対応します。
アニーリングマシンと問題設定 #
上述したような方針で問題を QUBO 形式で表現し、それを実際にアニーリングマシンに送信して解いてみます。今回はアニーリングマシンとしてD-Wave の量子アニーリングマシン D-Wave 2000Q と、富士通のアニーリングマシン 富士通デジタルアニーラ を用いました。以下が今回の問題設定です。
都市数: #
- D-Wave 2000Q: 8
- 富士通デジタルアニーラ: 25
- 都市の位置: 2次元平面上にランダム生成
- 都市間の距離は位置からユークリッド距離を計算
結果 #
D-Wave 2000Q #
D-Wave 2000Q では8都市の巡回セールスマン問題を解きました。内部的に 1000 回実行した結果のうちエネルギーが最小のものを図示すると、ランダムに生成した7つの問題について以下の図のようになりました。
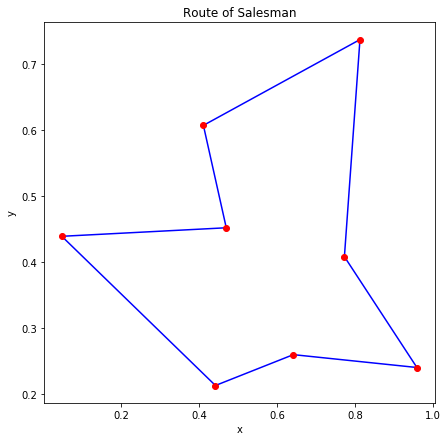
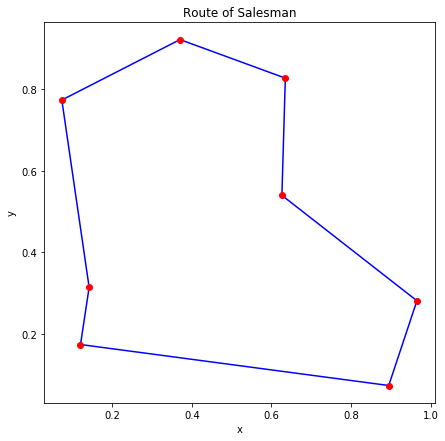
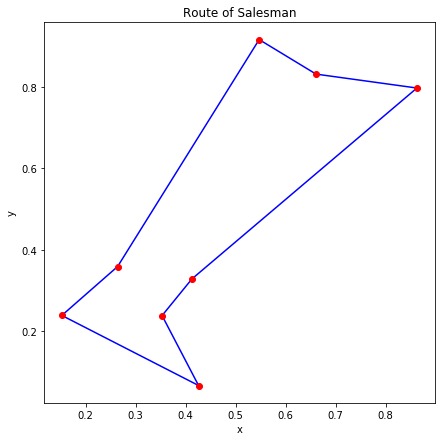
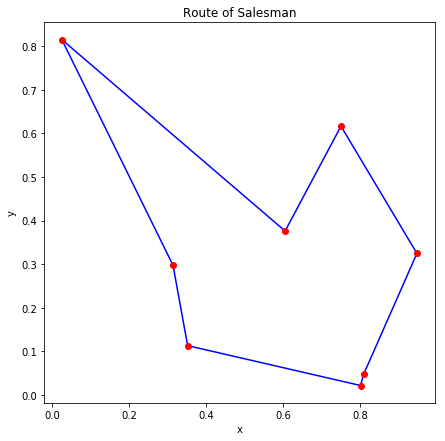
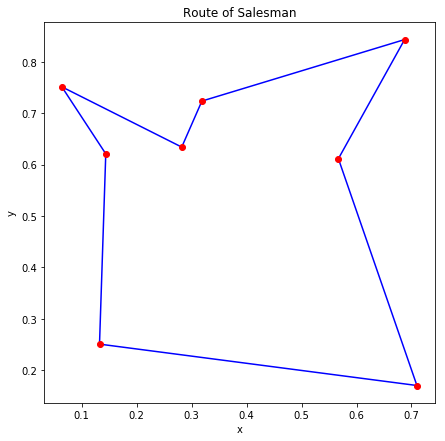
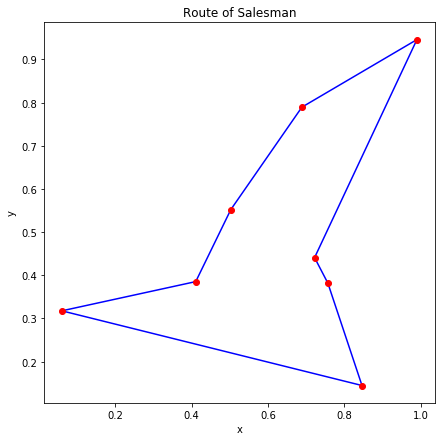
概ね良さそうな解が得られているように見えます。
富士通デジタルアニーラ #
富士通デジタルアニーラでは使用可能な全結合ビット数は1024ビットです。これは32都市の巡回セールスマン問題に対応しますが、パラメータの調整が難しいため、今回は25都市の巡回セールスマン問題を解きました。
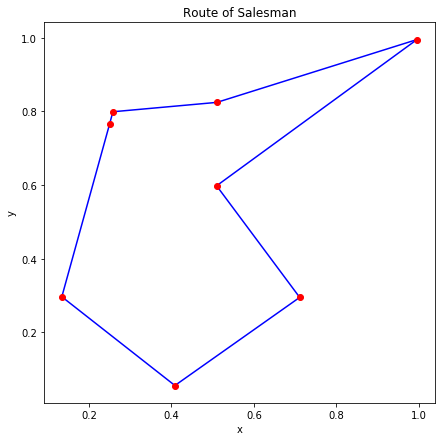
内部的に 20 回実行したうちエネルギーが最小のものを図示すると、ランダムに生成した7つの問題について以下の図のようになりました。
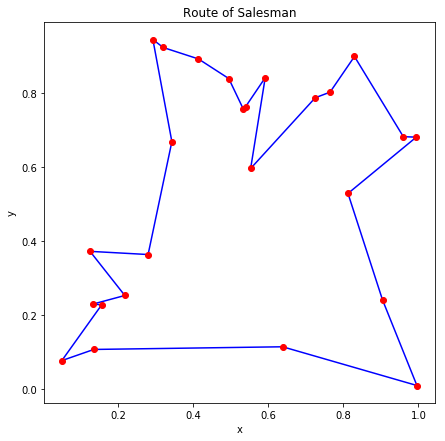
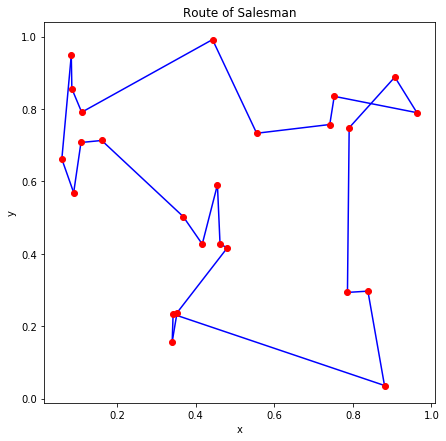
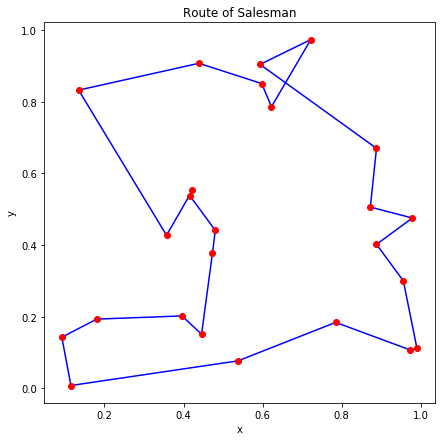
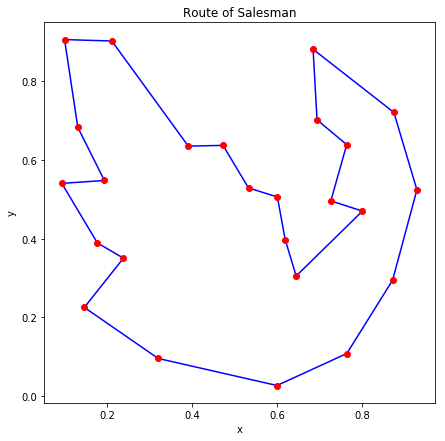
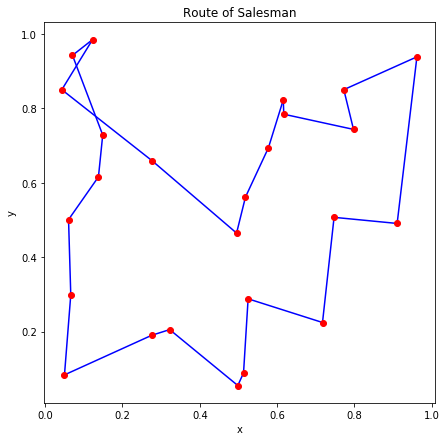
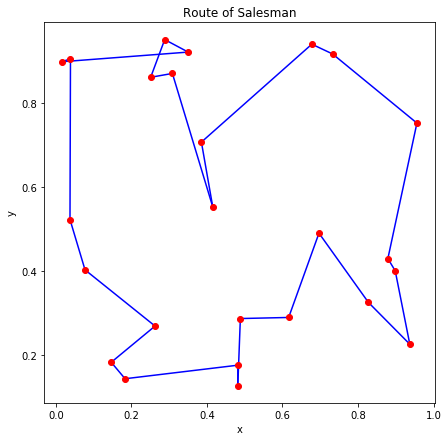
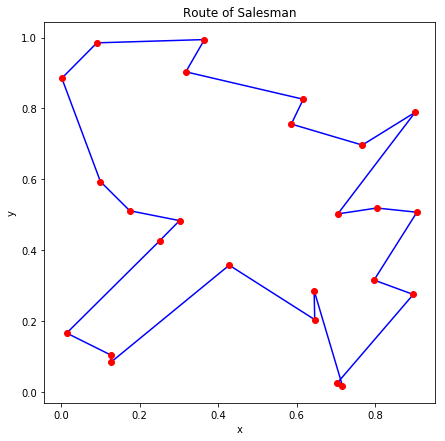
これらも多少の手直しを加えれば最適解に近い解が得られるように見えます。
最後に #
巡回セールスマン問題は「全ての都市を1回ずつ訪れて元の地点に戻ってこなければならない」という複雑な制約条件があり、 \(0\) と \(1\) しか取ることのできない QUBO 変数とその積で表わされる相互作用で表現するのは一見難しそうに見えます。しかし、一度に考えるのは難しくても、まずは問題をナイーブに構築しその後で制約条件を課すことで、問題を考えやすくすることが出来ました。
これはアニーリングマシンを使いこなす上での基本的な考え方です。そのため、巡回セールスマン問題の構築方法を理解しておくことは、様々な応用を考える上での導入的な良い題材となっています。